試問有多少個整數 $x$ 滿足 $2\left|x\right|+x\lt 10$？

某燈會布置變色閃燈，每次啟動後的閃燈顏色會依照以下的順序做週期性變換：藍-白-紅-白-藍-白-紅-白-藍-白-紅-白…，每四次一循環，其中藍光每次持續 5 秒，白光每次持 續 2 秒，而紅光每次持續 6 秒。假設換燈號的時間極短可被忽略，試選出啟動後第 99 至 101 秒之間的燈號。

有八棟大廈排成一列，由左至右分別編號 $1,2,3,4,5,6,7,8$。今電信公司想選取其中三棟大廈的屋頂分別設立一座電信基地台。若基地台不能設立於相鄰的兩棟大廈，以免訊號互相干擾，試問在 $3$ 號大廈不設立基地台的情況下，有多少種設立基地台的選取方法？

在坐標平面上，已知向量 $\overrightarrow{PQ}=\Big ( log{\large\frac{1}{5},\normalsize-10^{-5}} \Big )$，其中點 $P$ 的坐標為 $\Big ( log{\large\frac{1}{2},\normalsize2^{-5}} \Big )$。試選出正確的選項。

設矩陣 $A=\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}$，若 $A^{7}-3A={\left[\begin{array}{l l}{a}&{b}\\ {c}&{d}\end{array}\right]}$，則 $a+b+c+d$ 之值為下列哪一個選項？

假設地球為一半徑 $r$ 的球體，有一質點自甲地沿著該地所在經線往北移動，抵達北極點時移動所經過的弧線之長度為 ${\large\frac{7}{12}}{\pi r}$。試問哪一個選項最可能是甲地的位置？

畫家把空間景物用單點透視法畫在平面的畫紙上時，有以下原則要遵守：
一、空間中的直線畫在畫紙上必須是一條直線。
二、空間直線上點的相關位置必須和畫紙所畫的點的相關位置一致。
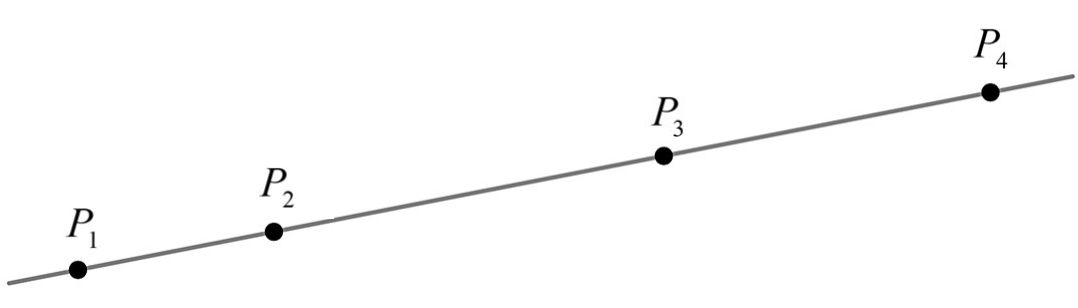
三、空間直線上的任四個相異點的 $K$ 值，和畫紙所畫的四個點之 $K$ 值必須相同，其中 $K$ 值的定義如下：直線上任給四個有順序的相異點 $P_{1},P_{2},P_{3},P_{4}$，如下圖。
其所對應的 $K$ 值定義為
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\Large K=\frac{\overline {P_1P_4} \times \overline {P_2P_3}}{\overline {P_1P_3} \times \overline {P_2P_4}}$ 。

今某畫家依照以上原則，將空間中一直線及該線上的四相異點 $Q_{1},Q_{2},Q_{3},Q_{4}$ 描繪在畫紙上，其中 ${\overline{{Q_{1}Q_{2}}}}={\overline{{Q_{2}Q_{3}}}}={\overline{{Q_{3}Q_{4}}}}$。若將畫紙上所畫的直線視為一數線，並將線上的點用坐標來表示，則在下列選項的四個坐標中，試問哪一組最可能是該四點在畫紙上的坐標？

有一射擊遊戲，將發射台設置於坐標平面的原點，並放置三個半徑為 1 的圓盤靶子，其圓心分別為 $(2,2)$、$(4,6)$ 與 $(8,1)$。玩家選定一正數 $a$，並按下按鈕後，發射台將向點 $(1,a)$ 方向發射一道雷射光束（形成一射線）。假設雷射光束擊中靶子後可以穿透並繼續沿原方向前進（削過圓盤邊緣也視為擊中）。試選出正確的選項。

設 $f(x)=2x^{3}-3x+1$，下列關於函數 $y=f(x)$ 的圖形之描述，試選出正確的選項。

甲、乙兩班各有 40 位同學參加某次數學考試（總分為 100 分），考試後甲、乙兩班分別以 $y_{1}=0.8x_{1}+20$ 和 $y_{2}=0.75x_{2}+25$ 的方式來調整分數，其中 $x_1,x_2$ 分別代表甲、乙兩班的原始考試分數，$y_1,y_2$分別代表甲、乙兩班調整後的分數。已知調整後兩班的平均分數均為 60 分，調整後的標準差分別為 16 分和 15 分。試選出正確的選項。

考慮坐標平面上的點 $O(0,0)$、$A$、$B$、$C$、$D$、$E$、$F$、$G$，如下圖所示： 其中 $B$ 點、$C$ 與 $D$ 點、$E$ 與 $F$ 點、$G$ 與 $A$點依序在一、二、三、四象限內。若 $\overrightarrow{{v}}$ 為坐標平面上的向量，且滿足 $\overrightarrow{v} \cdot \overrightarrow{OA} \gt 0$ 及 $\overrightarrow{v} \cdot \overrightarrow{OB} \gt 0$，則 $\overrightarrow{{v}}$ 與下列哪些向量的內積一定小於 $0$？

設 $a,b,c$ 都是非零的實數，且二次方程式 $ax^{2}+b x+c=0$ 的兩根都落在 1 和 3 之間。試選出兩根必定都落在 4 和 5 之間的方程式。

若 $x,y$ 為兩正實數，且滿足 $x^{{\frac{-1}{3}}}y^{2}=1$ 及 $2\log y=1$，則 $\large \frac{x-y^{2}}{10}=$ 。

坐標平面上有一個半徑為 7 的圓，其圓心為 $O$ 點。已知圓上有 $A,B$ 兩點，且 ${\overline{{A B}}}=8$，則內積 ${\overrightarrow{{OA}}}\cdot{\overrightarrow{{OB}}}=$ 。

根據某國對失蹤輕航機的調查得知：失蹤輕航機中有 70% 後來會被找到，在被找到的輕航機當中，有 60% 裝設緊急定位傳送器；而沒被找到的失蹤輕航機當中，則有 90% 未裝設緊急定位傳送器。緊急定位傳送器會在飛機失事墜毀時發送訊號，讓搜救人員可以定位。現有一架輕航機失蹤，若已知該機有裝設緊急定位傳送器，則它會被找到的機率為 。（化為最簡分數）

袋中有藍、綠、黃三種顏色的球共 10 顆。今從袋中隨機抽取兩顆球（每顆球被抽中的機率相等），若抽出的兩顆球皆為藍色的機率為 $\large\frac{1}{15}$，皆為綠色的機率為 $\large\frac{2}{9}$，則從袋中隨機抽出兩球，此兩球為相異顏色的機率為 。（化為最簡分數）

有三女三男共六位在校時和老師常有互動的同學，畢業後老師邀聚餐，餐後七人站一橫排照相留念。已知同學中有一女一男兩位曾有過不愉快，照相時不想相鄰，而老師站在正中間且三位男生不完全站在老師的同一側，則可能的排列方式共有 種。

瘦長的塔因為年代久遠，塔身容易傾斜。在下方右圖中，以粗黑線條代表塔身，而塔身的長度稱為塔高，塔身與鉛直虛線的夾角 $\theta^{\circ}$ 稱為該塔的傾斜度（ $0\leq\theta\lt 90$ ），又塔頂至鉛直虛線的距離稱為該塔的偏移距離。 根據上述資料，試回答下列問題。